2B Lab 2 Week 3

This is the pair coding activity related to Chapter 9.

Task 1: Open the R project for the lab

Task 2: Create a new `.Rmd` file

… and name it something useful. If you need help, have a look at Section 1.3.

Task 3: Load in the library and read in the data

The data should already be in your project folder. If you want a fresh copy, you can download the data again here: data_pair_coding.

We are using the packages tidyverse and correlation today. If you have already worked through this chapter, you will have all the packages installed. If you have yet to complete Chapter 9, you will need to install the package correlation (see Section 1.5.1 for guidance if needed).

We also need to read in dog_data_clean_wide.csv. Again, I’ve named my data object dog_data_wide to shorten the name but feel free to use whatever object name sounds intuitive to you.

Task 4: Tidy data & Selecting variables of interest

Step 1: Select the variables of interest. We need 2 continuous variables today, so any of the pre- vs post-test comparison will do. I would suggest happiness ratings (i.e., SHS_pre, SHS_post). Also keep the participant id RID. Store them in a new data object called dog_happy.

Step 2: Check for missing values and remove participants with missing in either pre- or post-ratings.

Step 3: Convert participant ID into a factor

Solution for Tasks 3 and 4

## Task 3
library(tidyverse)
library(correlation)

dog_data_wide <- read_csv("dog_data_clean_wide.csv")


## Task 4
dog_happy <- dog_data_wide %>%
  # Step 1
  select(RID, SHS_pre, SHS_post) %>% 
  # Step 2
  drop_na() %>% 
  # Step 3
  mutate(RID = factor(RID))

Task 5: Re-create the scatterplot below

`geom_smooth()` using formula = 'y ~ x'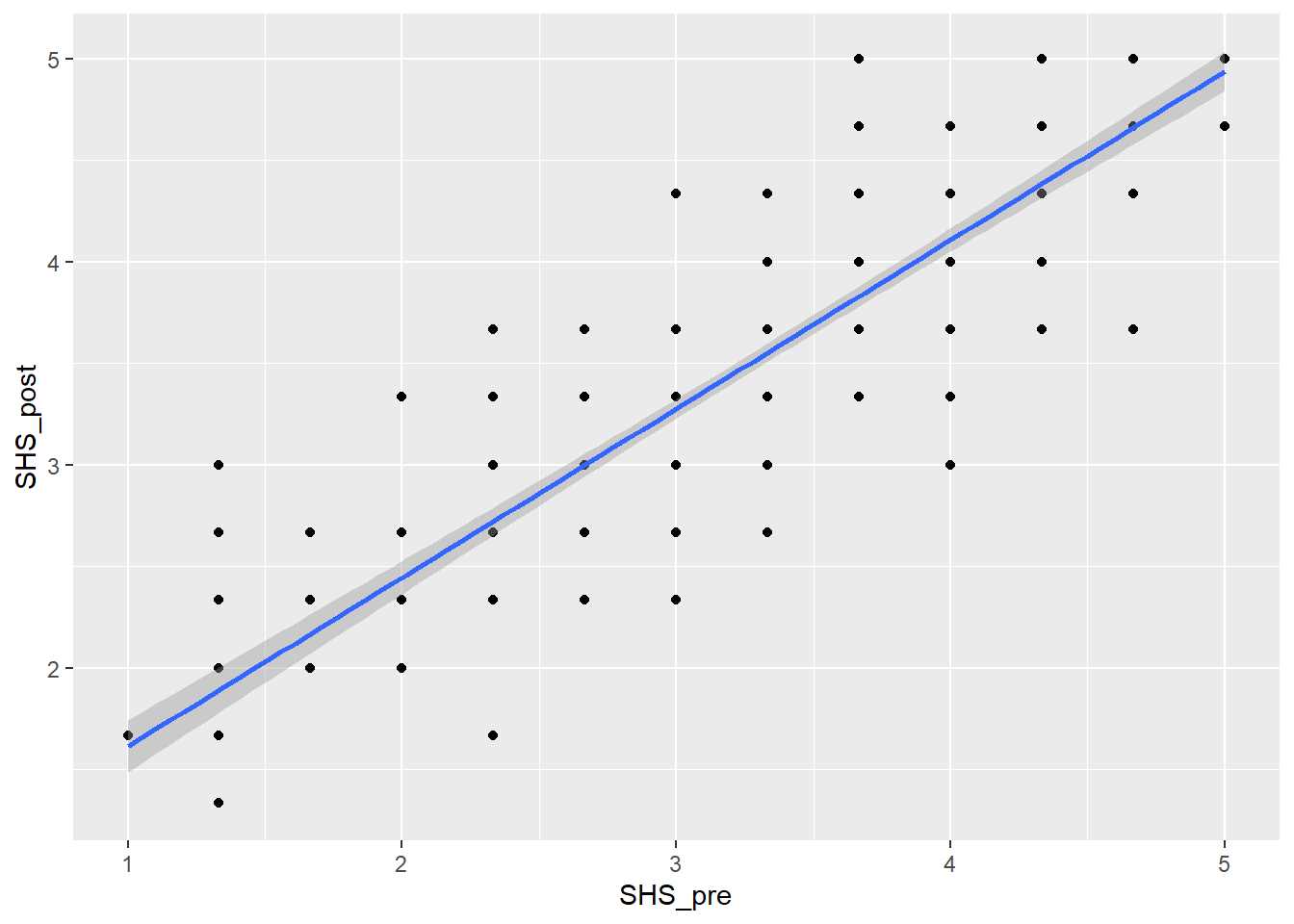

Solution

ggplot(dog_happy, aes(x = SHS_pre, y = SHS_post)) +
  geom_point() +
  geom_smooth(method = "lm")

Task 6: Assumptions check

We can either do the assumption check by looking at the scatterplot above or we can run the code plot(lm(SHS_pre~SHS_post, data = dog_happy)) and assess the assumptions there. Either way, it should give you similar responses.

Linearity: a relationship
Normality: residuals are
Homoscedasticity: There is
homoscedasticity as there is no distinct pattern in the residualsheteroscedasticity as the residuals show a distinct pattern
Outliers:

What is your conclusion from the assumptions check?

All assumptions hold. Therefore, we are conducting a parametric test, specifically Pearson’s correlation.Some assumptions are violated. Therefore, we are conducting a non-parametric test, specifically Spearman’s correlation.All assumptions are violated. Therefore, we are conducting a non-parametric test, specifically Spearman’s correlation.

Task 7: Compute a Pearson correlation & interpret the output

Step 1: Compute the Pearson correlation. The structure of the function is as follows:

correlation(data = your_dataframe,
            select = "variable1",
            select2 = "variable2",
            method = "Pearson",
            alternative = "two.sided")

The default method argument is Pearson, but if you thought any of the assumptions were violated and conduct a Spearman correlation instead, change the method argument to”Spearman”.

Solution

correlation(data = dog_happy,
            select = "SHS_pre",
            select2 = "SHS_post",
            method = "Pearson",
            alternative = "two.sided")

Parameter1	Parameter2	r	CI	CI_low	CI_high	t	df_error	p	Method	n_Obs
SHS_pre	SHS_post	0.8842169	0.95	0.855856	0.9072765	31.73394	281	0	Pearson correlation	283

# alternative because there are only 2 numeric columns in `dog_happy`
correlation(dog_happy)

Step 2: Interpret the output

A Pearson correlation revealed a , , and statistically relationship between happiness before and after the dog intervention, r() = , p , 95% CI = [, ]. We therefore .

Important

In the write-up paragraph above, the open fields accepted answers with 2 or 3 decimal places as correct. However, in your reports, ensure that correlation values are reported with 3 decimal places.