2B Lab 1 Week 2

This is the pair coding activity related to Chapter 8.

Task 1: Open the R project for the lab

Task 2: Create a new .Rmd file

… and name it something useful. If you need help, have a look at Section 1.3.

Task 3: Load in the library and read in the data

The data should already be in your project folder. If you want a fresh copy, you can download the data again here: data_pair_coding.

We are using the packages rstatix, tidyverse, qqplotr, lsr today. Make sure to load rstatix in before tidyverse.

We also need to read in dog_data_clean_wide.csv. Again, I’ve named my data object dog_data_wide to shorten the name but feel free to use whatever object name sounds intuitive to you.

For the plot, we will need the data in long format. We can either read in dog_data_clean_long.csv to take a shortcut, or wrangle the data from dog_data_wide. I’ve taken the shortcut and named my data object dog_data_long.

Task 4: Tidy data for a paired t-test

Not much tidying to do for today.

Pick a variable of interest and select the pre- and post-scores, and calculate the difference score. Store them in a separate data object with a meaningful name.

I will use Loneliness as an example and call my data object dog_lonely. Regardless of your chosen variable, your data object should look like/ similar to the table below.

RID Loneliness_pre Loneliness_post Loneliness_diff
1 2.25 1.70 -0.55
2 1.90 1.60 -0.30
3 2.25 2.25 0.00
4 1.75 2.05 0.30
5 2.85 2.70 -0.15

In dog_data_long, we want to turn Stage into a factor so we can re-order the labels (i.e., “pre” before “post”).

## Task 3
library(rstatix)
library(tidyverse)
library(lsr)

dog_data_wide <- read_csv("data/dog_data_clean_wide.csv")
Rows: 284 Columns: 24
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr  (3): GroupAssignment, Year_of_Study, Live_Pets
dbl (21): RID, Age_Yrs, Consumer_BARK, Flourishing_pre, Flourishing_post, PA...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
dog_data_long <- read_csv("data/dog_data_clean_long.csv")
Rows: 568 Columns: 16
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr  (4): GroupAssignment, Year_of_Study, Live_Pets, Stage
dbl (12): RID, Age_Yrs, Consumer_BARK, Flourishing, PANAS_PA, PANAS_NA, SHS,...

ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
## Task 4
dog_lonely <- dog_data_wide %>% 
  select(RID, Loneliness_pre, Loneliness_post) %>% 
  mutate(Loneliness_diff = Loneliness_post - Loneliness_pre)

dog_data_long <- dog_data_long %>% 
  mutate(Stage = factor(Stage,
                        levels = c("pre", "post")))

Task 5: Compute descriptives

We want to determine the mean and sd of:

  • the pre-scores
  • the post-scores, and
  • the difference scores

Store them in a data object called descriptives.

descriptives <- dog_lonely %>% 
  summarise(mean_pre = mean(Loneliness_pre),
            sd_pre = sd(Loneliness_pre),
            mean_post = mean(Loneliness_post),
            sd_post = sd(Loneliness_post),
            diff = mean(Loneliness_diff),
            sd_diff = sd(Loneliness_diff))

Task 6: Check assumptions

Assumption 1: Continuous DV

Is the dependent variable (DV) continuous? Answer:

Assumption 2: Data are independent

Each pair of values in the dataset has to be independent, meaning each pair of values needs to be from a separate participant. Answer:

Assumption 3: Normality

Looking at the violin-boxplots below, do you think the assumption of normality holds?

Note

The axis label of Plot 2 turned out to be quite long here. I’ve used the escape character \n to break it up across 2 lines.

## Plot 1
ggplot(dog_data_long, aes(x = Stage, y = Loneliness, fill = Stage)) +
  geom_violin(alpha = 0.5) +
  geom_boxplot(width = 0.4, alpha = 0.8) +
  scale_fill_viridis_d(guide = "none") +
  theme_classic() +
  labs(x = "Time point", y = "mean Loneliness Scores")

## Plot 2
ggplot(dog_lonely, aes(x = "", y = Loneliness_diff)) +
  geom_violin(fill = "#21908C", alpha = 0.5) +
  geom_boxplot(fill = "#21908C", width = 0.4) +
  theme_classic() +
  labs(x = "",
       y = "Difference in mean Loneliness scores \nbetween pre- and post- intervention") # \n forces a manual line break in the axis label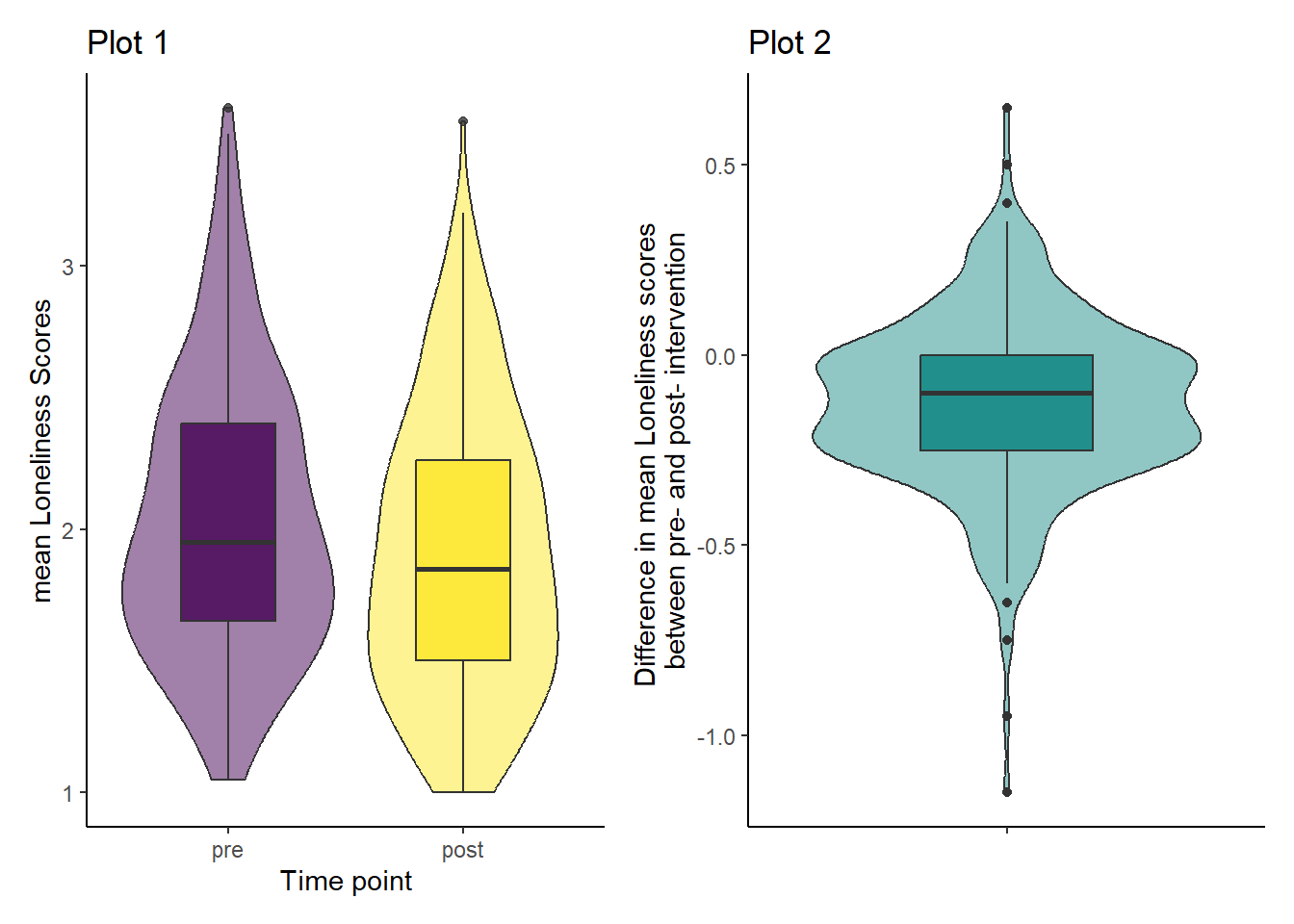

Plots displayed to assess normality assumption

Answer:

Conclusion from assumption tests

With all assumptions tested, which statistical test would you recommend for this analysis?

Answer:

Task 7: Computing a paired-sample t-test with effect size & interpret the output

  • Step 1: Compute the paired-sample t-test. The structure of the function is as follows:
t.test(your_data$var1, your_data$var2, paired = TRUE)
t.test(dog_lonely$Loneliness_pre, dog_lonely$Loneliness_post, paired = TRUE)
  • Step 2: Calculate an effect size

Calculate Cohen’s D. The structure of the function is as follows:

cohensD(your_data$var1, your_data$var2, method = "paired")
cohensD(dog_lonely$Loneliness_pre, dog_lonely$Loneliness_post, method = "paired")
  • Step 3: Interpreting the output

Below are the outputs for the descriptive statistics (table), paired-samples t-test (main output), and Cohen’s D (last line starting with [1]). Based on these, write up the results in APA style and provide an interpretation.

mean_pre sd_pre mean_post sd_post diff sd_diff
2.040187 0.5304488 1.914298 0.5344914 -0.1258895 0.2290269 

    Paired t-test

data:  dog_lonely$Loneliness_pre and dog_lonely$Loneliness_post
t = 9.2632, df = 283, p-value < 2.2e-16
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 0.09913876 0.15264034
sample estimates:
mean difference 
      0.1258895 
[1] 0.5496716

We hypothesised that there would be a significant difference between Loneliness measured before (M = , SD = ) and after (M = , SD = ) the dog intervention. On average, participants felt less lonely after the intervention (Mdiff = , SDdiff = ). Using a paired-samples t-test, the effect was found to be and of a magnitude, t() = , p , d = . We therefore .